Monte Carlo integration

We have seen a few techniques to integrate a one-dimensional function. For integration in larger numbers of dimensions we face a problem:

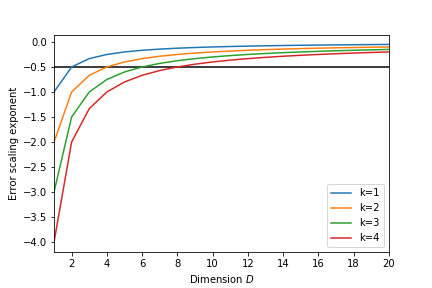
• If we want to sample each dimension with $N$ points we need $N_{total}=N^D$ points
• The error scales as a function of $\Delta t=L/N$ like $\Delta t^k$ where $k$ is related to the order of the approximation
• the error therefore scales as

$$ N^{-k} = N_{total}^{-k/D} $$

We can see that for large dimensions the scaling is quite poor!

Monte Carlo integration

We can abandon the requirement of sampling along a fixed size grid and sample points randomly.

The Monte Carlo integration approximation for the integral is given by:

$$ \int_\Omega f(x) \;dx = \frac{V}{N} \sum\limits_{i=1}^N f(r_i) $$

with

$$ V = \int_\Omega \;dx $$

Convergence

Look at function

$$ f(x) = \prod_i x_i $$

And we integrate it over the unit cube in $D$ dimensions:

$$ I_D = \int_0^1 dx_1 \dots \int_0^1 dx_D\; x_1 \dots x_D = 2^{-D} $$

Now plot the error

$$ E(D) = \left| 2^D I_D -1 \right|$$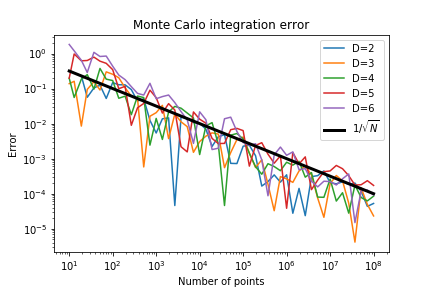

The error scales as $1/\sqrt{N_{total}}$ regardless of the dimension!

For high dimensions this is going to be better than regular sampling!