Random walks

A random walk is a trajectory made by taking consecutive random steps.

The choice of step is uncorrelated with the previous steps, but it can be done according to a non-uniform probability

Examples

• physics:
  • molecule movement in gas/liquid
• life:
  • crowds
  • stock market (sometimes)
• biology:
  • bacteria movement

1-D random walk

At each step we decide whether to move in the positive direction or in the negative direction with equal probability.

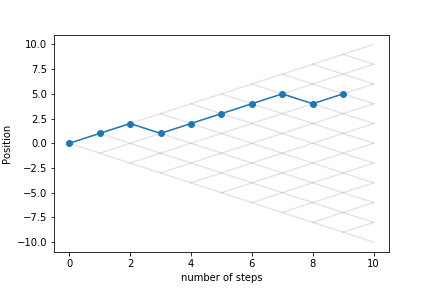
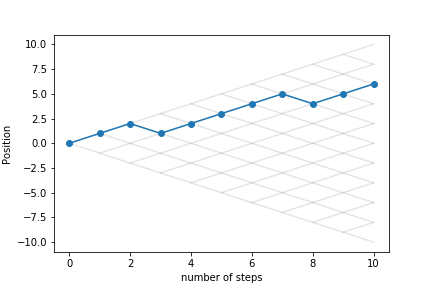
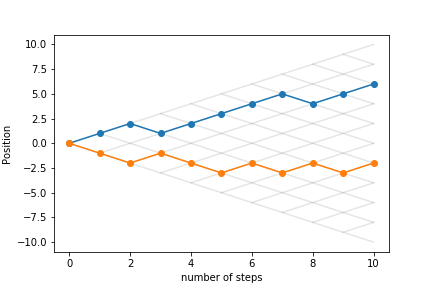
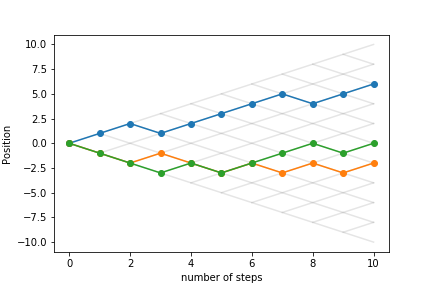
Let's look at other trajectories:

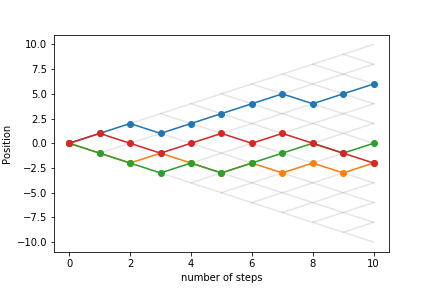
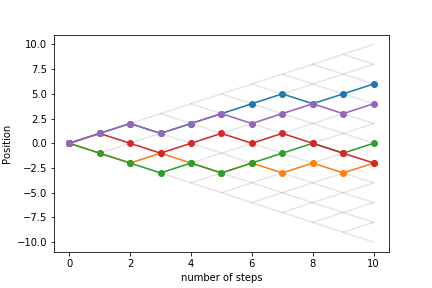
Continuum behaviour

Individual walkers have a random behaviour but collectively they have some statistical properties.

Similar to the case of the radioactive decay where each atom is independent.

100 walkers with 100 steps:

1000 walkers with 100 steps:

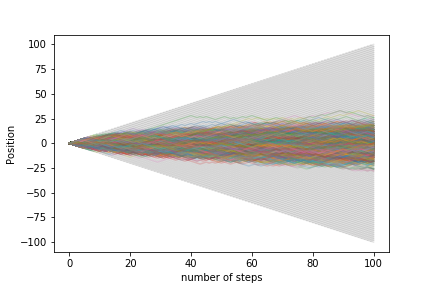
To quantify if let's look at the average position and the standard deviation as a function of the number of steps:

$$\bar x = \left<x\right> \;, \qquad \left<(x-\bar x)^2\right>$$

average position

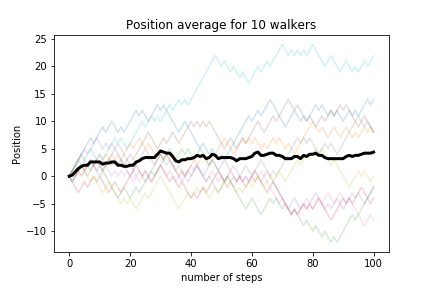
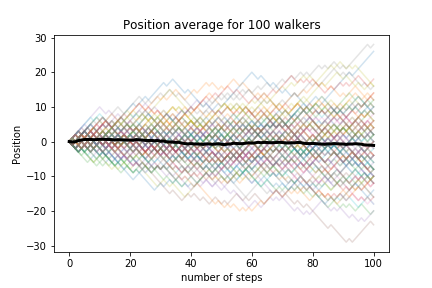
The average position is zero. Let's look at the squared distance:

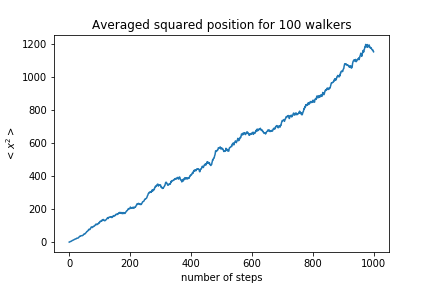
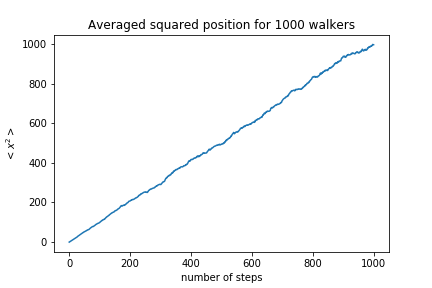
The squared distance is proportional to the number of steps, which means the standard deviation of the walkers position scales like $\sqrt{N}$.

This matches the properties of the solutions of the diffusion equation

$$\frac{\partial \rho}{\partial t} = D \Delta \rho \;,\qquad \Delta \rho = \sum_i \frac{\partial^2\rho}{\partial x_i^2} $$

So random walks are suitable to model diffusion processes.

Random walks in multiple dimensions

We can have random walks in more than one dimension

• at each step we decide
  • in which dimension to move
  • whether to move in the positive or negative direction

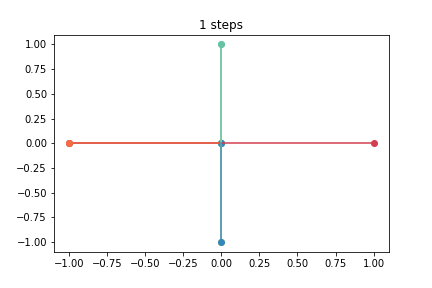
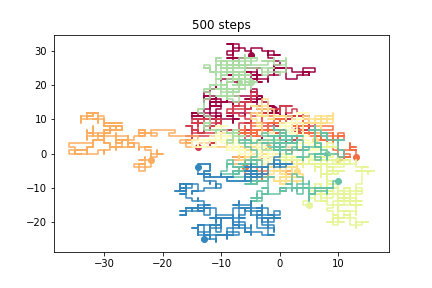
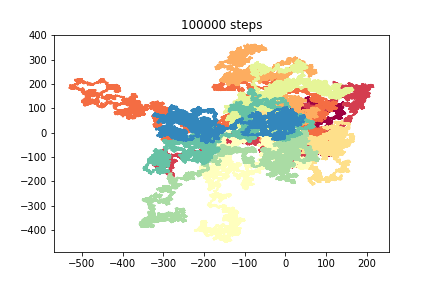
3D walkers

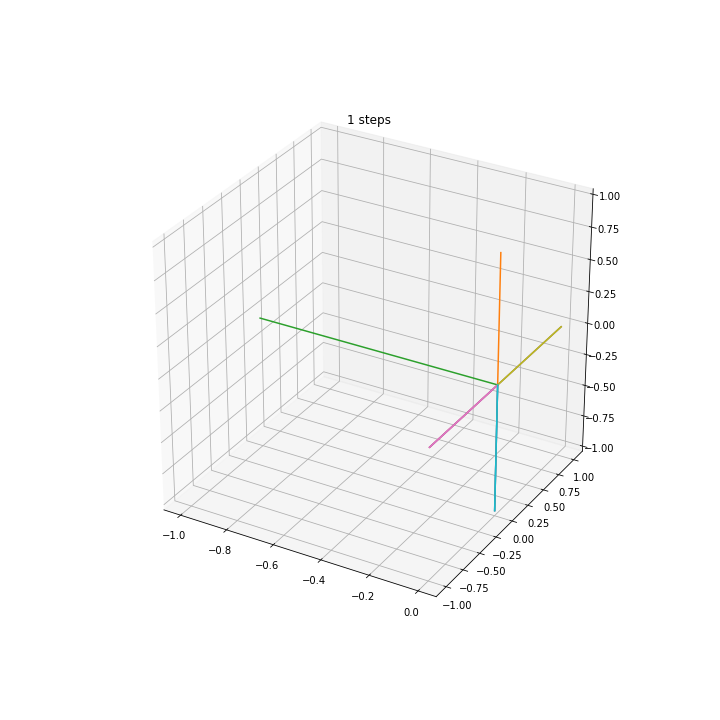
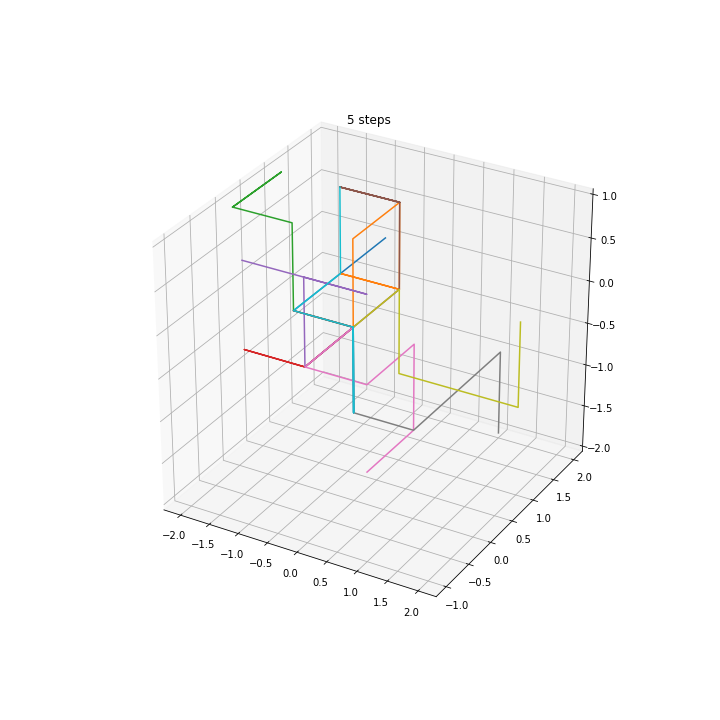
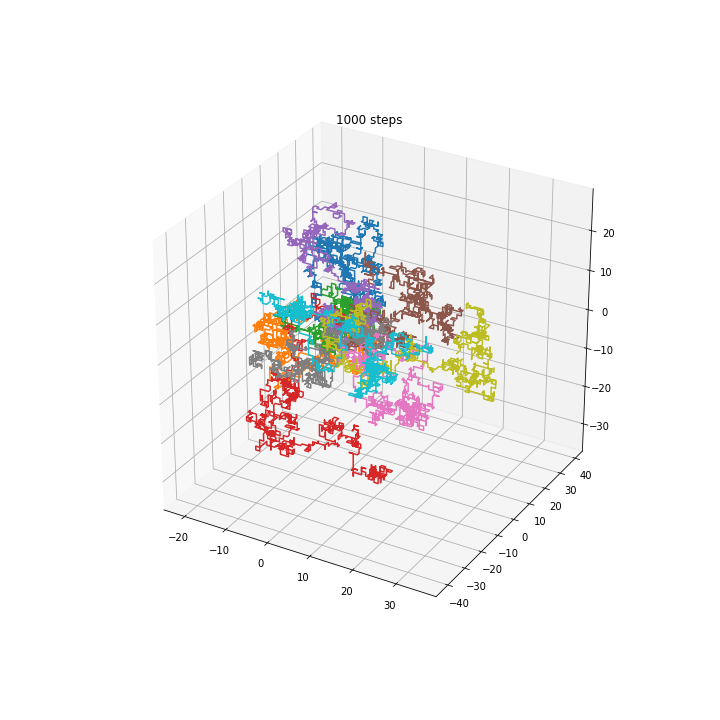
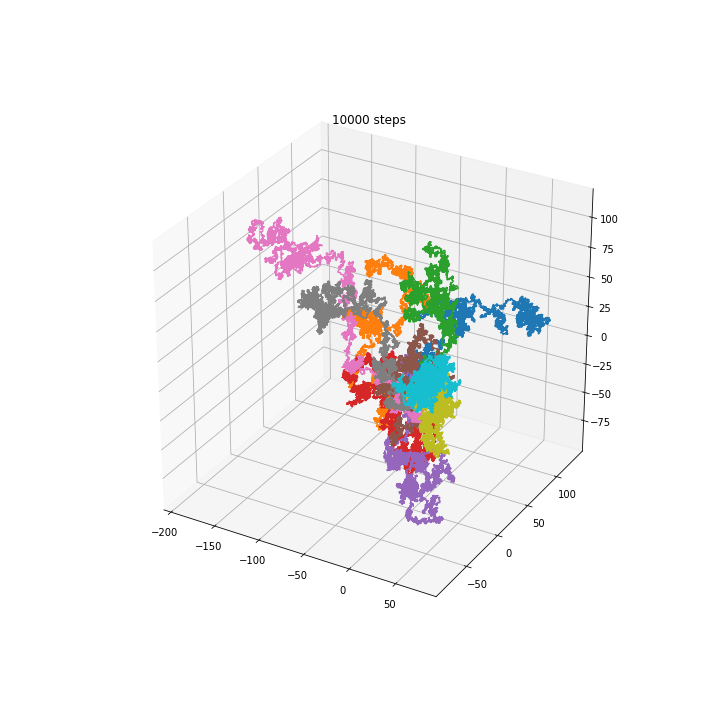
Squared distance in multiple dimensions

The scaling of the squared distance as a function of the number of steps is the same in all dimensions: