Numerical precision

import matplotlib.pyplot as plt
import numpy as np

For numerical application computers store numbers with a finite precision.

  • limited memory available
  • limited processing power

This can lead to problems when numbers with large magnitude difference are combined

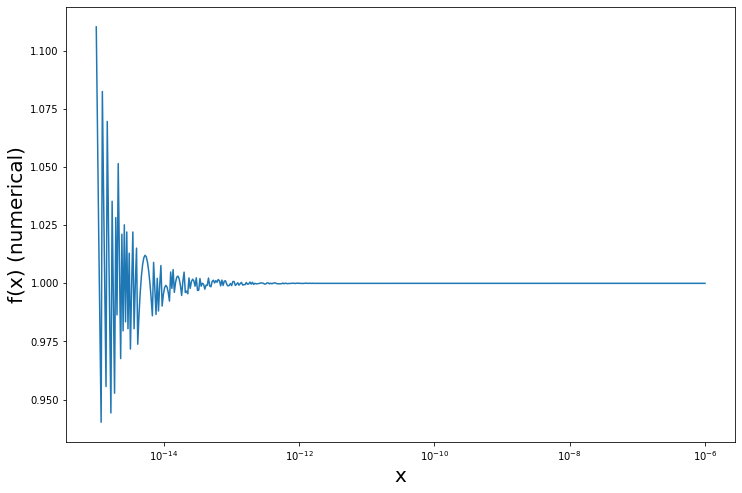
Let’s look at the function

$$f(x)= \frac{(1+x) - 1}{x}=1$$

This should always return 1. But if $x$ is very small we get in trouble when we use this function numerically on a computer.

def f(x):
    return ((1.0 + x) - 1.0) / x 

plt.figure(figsize=(12,8))
exps = np.linspace(-6,-15,500)
xs = 10.0**(exps)
plt.plot(xs,f(xs))
plt.xscale('log')
plt.xlabel('x',fontsize=20)
plt.ylabel('f(x) (numerical)',fontsize=20);

Explanation

Floating point numbers are stored in the form

\(\pm m \cdot 2^e\) where \(1\leq m < 2\)

Let's first consider a decimal number \(x=0.0123456789\) that we want to represent in a computer. In a hypothetical computer that uses base ten and has only 5 digits of precision (in contrast to the typical 16 decimal digits of precision), the number might be truncated to \(x=0.012345\).

However, computers fundamentally operate in binary. In binary, numbers are expressed using only the digits '0' and '1'. To convert \(x\) to binary, it might look like \(0.000000110001111011\ldots \times 2^{-6}\). Notice that this is still an approximation.

In a simplified computer system that uses 5 bits of precision for \(m\) and \(e\), this binary representation would be truncated, something like \(0.00000 \times 2^{-6}\), further emphasizing the importance of understanding how floating-point numbers are stored and the associated errors.

The decimal representation would be

$x=1.23457\cdot 10^{-2}$

Let’s start evaluating $1+x$:

$1+0.0123457 = 1.0123457$

which is represented as

$1.01235 \cdot 10^0 $

Now we subtract $1$:

$1.01235 - 1 = 0.01235 $

which is represented as

$1.235\star\star \cdot 10^{-2}$

where the $\star$ have to be made up by the computer. It is done in a deterministic manner but they can’t be the right digits for all calculations.

If we now divide by the original $x$ to get $f(x)$ we get

$\frac{1.235\star\star\cdot 10^{-2}}{1.23457\cdot 10^{-2}} = 1.00\star\star\star$

We can see that instead of $1$ we get some “corruption”. This is not surprising as we would need 7 digits of precision to be able to carry out the calculation without loss.

  • Overflow: When the exponent \(e\) becomes too large for the given floating-point representation, leading to \(\infty\).
  • Underflow: When \(e\) is too small, leading to a representation of zero.

Numerical errors

  • this is a bit of a contorted example
  • in practice it is not always an issue
  • one has to be careful when considering “small number”
  • we will do this very often:
    • differentiating
    • integrating
  • we will need to tune our “small” numbers to be
    • small enough for the approximation to hold
    • large enough to avoid numerical round-off errors

Testing for equality

there are other pitfalls with numerical precision. The most common is that due to numerical round off errors values that should be equal are not! For example $$ \sum_1^{1000} \frac{1}{1000} \neq 1 $$

x=0.0
for i in range(1000):
    x+=0.001 
x == 1

False

x

1.0000000000000007

Testing for equality

It is better to:

  • Use inequalities
  • Calculate offsets rather than accumulating
  • Avoid subtraction of nearly equal numbers to mitigate catastrophic cancellation
xmin = 0
xmax = 1
n = 1000
delta = ( xmax - xmin ) / n

x\_accumulate = 0

for i in range(n):
    x\_accumulate += delta           # dangerous
for i in range(n):
    x\_calculate = xmin + i/float(n) * (xmax - xmin)  # better
  • Error Accumulation: Repeatedly adding a small number to a running total can accumulate errors in floating-point arithmetic. Example: x_accumulate += delta is more prone to error accumulation.
  • Numerical Stability: Calculating each value independently of the others, as in x_calculate = xmin + i/float(n) * (xmax - xmin), avoids this issue, offering better numerical stability.

Slightly more Realistic Example

In particle physics we often need the velocity in terms of the speed of light $$\beta = \sqrt{1-m^2/E^2},$$ where $m$ is the particle mass and $E$ its energy in natural units.

We often need to evaluate $$1-\beta,$$ for $E\gg m$ so that $$1-\beta\to \frac{m^2}{2E^2}.$$

plt.figure(figsize=(12,6))
energy = np.logspace(-3.292,6,1000)
m = 0.51e-3
def oneMinusBeta(x):
    return 1.-np.sqrt(1.-m**2/x**2)
plt.plot(energy,oneMinusBeta(energy))
plt.xscale('log')
plt.yscale('log')
plt.ylim([1e-20,1])
plt.xlabel('Energy [GeV]',fontsize=20)
plt.ylabel('$1-\\beta$',fontsize=20);

A more accurate form

Think about how you could rewrite $1-\beta$ in a way which is more numerically stable.

Hint

There’s two ways we can do this

  • One which always works is to replace the full expression with a series expansion for small $m/E$
  • One trick for this case is to use $1-\beta^2=\frac{m^2}{E^2}$ to rewrite $1-\beta$

Solution

So we could either write

  • $1-\beta\approx \frac{m^2}{2E^2}+\frac{m^4}{8E^4}$ valid for $m\ll E$
  • $1-\beta = \frac{m^2}{E^2(1+\beta)}$ valid for all $m$
def oneMinusBeta\_exp(x) :
    return np.where(x<100.*m,oneMinusBeta(x),
                       0.5*m**2/x**2+0.125*m**4/x**4)
def oneMinusBeta\_re(x) :
    return m**2/x**2/(1.+np.sqrt(1.-m**2/x**2))

plt.figure(figsize=(12,6))
energy = np.logspace(-3.292,6,1000)
m = 0.51e-3
plt.plot(energy,oneMinusBeta(energy),label='Naive')
plt.plot(energy,oneMinusBeta\_exp(energy),label='Expansion')
plt.plot(energy,oneMinusBeta\_re(energy),label='Rewrite',linestyle=':')
plt.xscale('log')
plt.yscale('log')
plt.ylim([1e-20,1])
plt.xlabel('Energy [GeV]',fontsize=20)
plt.legend()
plt.ylabel('$1-\\beta$',fontsize=20);
  • Catastrophic Cancellation: The original function is prone to loss of significant digits due to subtracting nearly equal numbers. For instance, the term 1.-np.sqrt(1.-m**2/x**2) is susceptible to this issue.
  • Conditional Approximation: The function oneMinusBeta_exp(x) employs a conditional approximation for x > 100 * m using the Taylor series expansion. This avoids the need for subtracting nearly equal terms, thus enhancing numerical stability.
  • Algorithmic Reformulation: The function oneMinusBeta_re(x) avoids direct subtraction operations that could lead to significant round-off errors. Instead, it uses division to combine terms, a less error-prone approach.
  • Square Root Instability: Square root operations, often seen in the original expressions, can lead to loss of significant digits, especially when the argument is close to 1. Both alternative functions carefully handle or circumvent square root operations to avoid this.
  • Numerical Analysis Techniques: Both functions embody principles from numerical analysis by algorithmically reformulating the expressions for greater numerical stability.