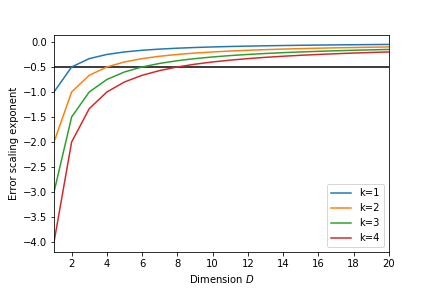
Monte Carlo integration
We have seen a few techniques to integrate a one-dimensional function. For integration in larger numbers of dimensions we face a problem:
- If we want to sample each dimension with $N$ points we need $N_{total}=N^D$ points
- The error scales as a function of $\Delta t=L/N$ like $\Delta t^k$ where $k$ is related to the order of the approximation
- the error therefore scales as $$ N^{-k} = N_{total}^{-k/D} $$
We can see that for large dimensions the scaling is quite poor!
We can abandon the requirement of sampling along a fixed size grid and sample points randomly.
The Monte Carlo integration approximation for the integral is given by:
$$ \int_\Omega f(x) ;dx = \frac{V}{N} \sum\limits_{i=1}^N f(r_i) $$
with
$$ V = \int_\Omega ;dx $$
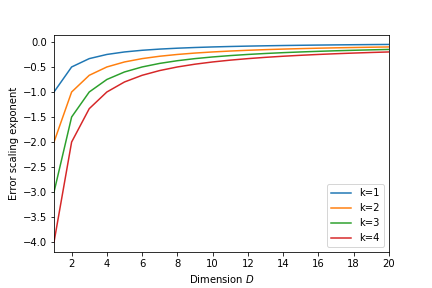
Convergence
Look at function
$$ f(x) = \prod_i x_i $$
And we integrate it over the unit cube in $D$ dimensions:
$$ I_D = \int_0^1 dx_1 \dots \int_0^1 dx_D; x_1 \dots x_D = 2^{-D} $$
Now plot the error
$$ E(D) = \left| 2^D I_D -1 \right|$$
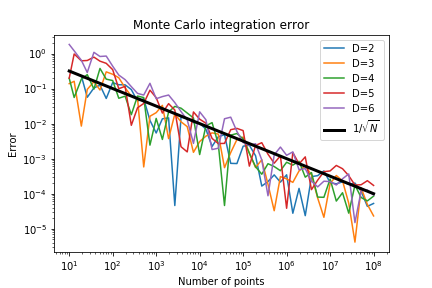
The error scales as $1/\sqrt{N_{total}}$ regardless of the dimension!
For high dimensions this is going to be better than regular sampling!