Finding the zeros of a function
We will consider numerical methods to find the value(s) of $x$ for which a $$ f(x) = 0 $$
for a continuous function $f$.
Newton-Raphson method
Let us denote the true root of $f(x)=0$ with $X$, so we have
$$f(X) = 0$$
We will devise an algorithm to find values $x_i$ that are estimates of $X$. We will denote the error in the estimate $x_i$ with $\Delta x_i$ so we have $$ X= x_i + \Delta x_i ;.$$
Suppose we know the derivative of $f$. We can expand $f$ around $x_i$:
$$ 0 = f(X) = f(x_i + \Delta x_i) = f(x_i) + \Delta x_i f^\prime(x_i) + \mathcal{O}(\Delta x_i^2) $$
We can now solve for $\Delta x_i $: $$ \Delta x_i = -\frac{f(x_i)}{f^\prime(x_i)} + \mathcal{O}(\Delta x_i^2)$$ Using this value we can get our next estimate of $X$: $$ x_{i+1} = x_{i} - \frac{f(x_i)}{f^\prime(x_i)} $$
Convergence
How good is the approximation?
$$\begin{eqnarray}\Delta x_{i+1} &=& \Delta x_i + \frac{f(x_i)}{f^\prime(x_i)}= \Delta x_i + \frac{f(X - \Delta x_i)}{f^\prime(X-\Delta x_i)}\\ &=&\Delta x_i + \frac{f(X) - \Delta x_i f^\prime(X)+ \frac12 \Delta x_i^2 f^{\prime\prime}(X)}{f^\prime(X) -\Delta x_i f^{\prime\prime}(X))} \\&=& \Delta x_i + \frac{ - \Delta x_i \left(f^\prime(X) - \Delta x_i f^{\prime\prime}(X) \right) - \frac12 \Delta x_i^2 f^{\prime\prime}(X)}{f^\prime(X) -\Delta x_i f^{\prime\prime}(X))} \\ &=& -\Delta x_i^2\frac{ f^{\prime\prime}(X)}{2 f^\prime(X)} +\mathcal{O}(\Delta x_i^3) \end{eqnarray}$$
The order of convergence is 2.
Secant method
If we do not know the derivative we can estimate it numerically using previous estimates:
$$ f^\prime(x_i)\approx \frac{f(x_i)-f(x_{i-1})}{x_i-x_{i-1}}$$
And use it instead of the derivative:
$$ x_{i+1} = x_{i} -f(x_i)\frac{x_i-x_{i-1}}{f(x_i)-f(x_{i-1})} $$
The convergence is slightly less good:
$$ \Delta x_{i+1} \approx -\frac{f^{\prime\prime}(X)}{2f^\prime(X)}\Delta x_i \Delta x_{i-1} $$
The rate of convergence is the golden ratio $(1+\sqrt{5})/2\sim 1.6$.
Bisection method
The methods based on the derivative can go wrong
- If the derivative of the function $f$ is badly behaved
- we start the algorithm too far away from a 0 and the expansion around $X$ is not representative of the function $f$.
We can use a more rudimentary method: bisection.
We need a value $x_+$ such that $f(x_+)>0$ and $x_-$ such that $f(x_-) < 0$ so we know the root $X$ is between the values $x_+$ and $x_-$.
We then evaluate $f(m)$ for
$$m=\frac{x_+ + x_-}{2}$$
and if $f(m)<0$ we replace $x_-$ with $m$, else we replace $x_+$ with $m$.
At each step the interval is halved. So the convergence is of order 1:
$$ \Delta x_{i+1}\approx \Delta x_i/2$$
Algorithm termination
All algorithms needs a criterium to finish:
- it is very unlikely that the algorithm will find the exact zero
- once you get very close numerical round-off errors get more important
Possibilities are, given a tolerance $\epsilon >0$:
- stop when the approximation of the zero doesn’t change much after iterations: $$| x_{i+1} - x_{i} | < \epsilon $$
- sometimes relative difference is better: $$ \left|\frac{x_{i+1}-x_{i}}{x_{i+1}+x_{i}}\right| < \epsilon $$
- stop when the function value is close enough to 0: $$ |f(x_i)| < \epsilon $$
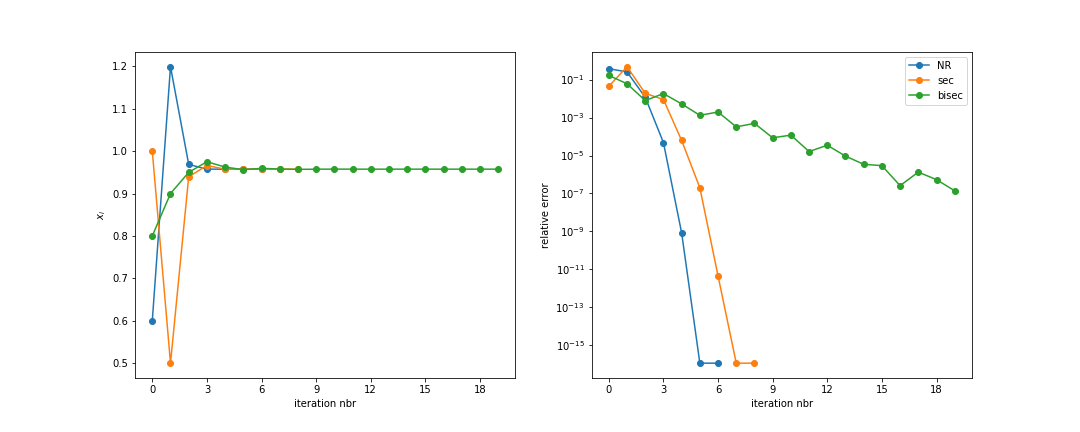
Example
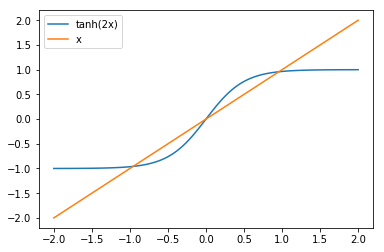
Consider the equation $ x = \tanh(2x)$
Look for the non-trivial zero around $x=1$.
import matplotlib.pyplot as plt
import numpy
xs = numpy.linspace(-2,2,100)
plt.plot(xs,numpy.tanh(2*xs), label="tanh(2x)")
plt.plot(xs,xs,label="x")
plt.legend();
Plot of root location and error for each method: