Random walks
A random walk is a trajectory made by taking consecutive random steps.
The choice of step is uncorrelated with the previous steps, but it can be done according to a non-uniform probability
Examples
- physics:
- molecule movement in gas/liquid
- life:
- crowds
- stock market (sometimes)
- biology:
- bacteria movement
1-D random walk
At each step we decide whether to move in the positive direction or in the negative direction with equal probability.

Let’s look at other trajectories:


Continuum behaviour
Individual walkers have a random behaviour but collectively they have some statistical properties.
Similar to the case of the radioactive decay where each atom is independent.
100 walkers with 100 steps:
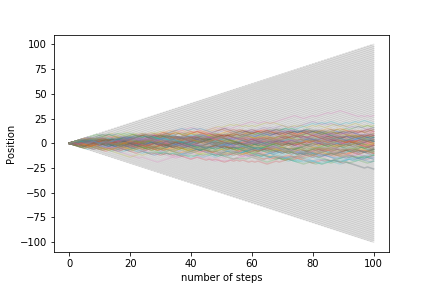
1000 walkers with 100 steps:
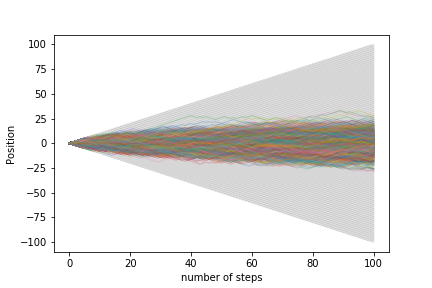
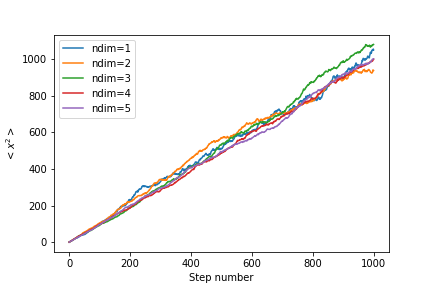
To quantify if let’s look at the average position and the standard deviation as a function of the number of steps:
$$\bar x = \left<x\right> ;, \qquad \left<(x-\bar x)^2\right>$$
average position
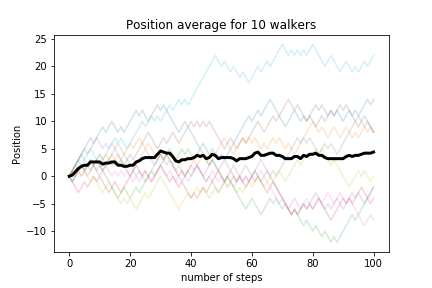
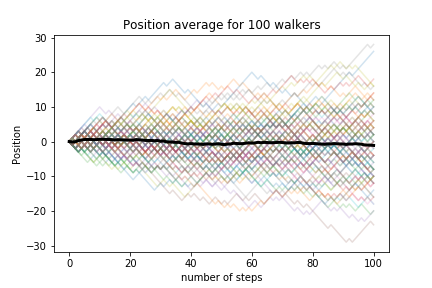
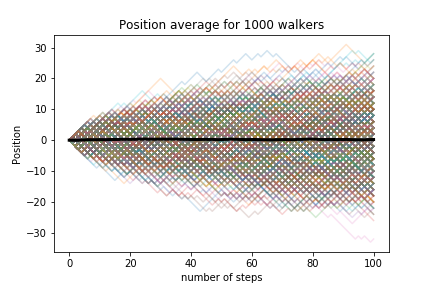
The average position is zero. Let’s look at the squared distance:
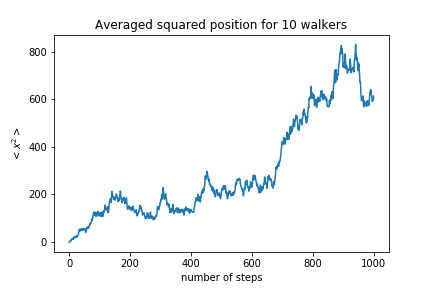
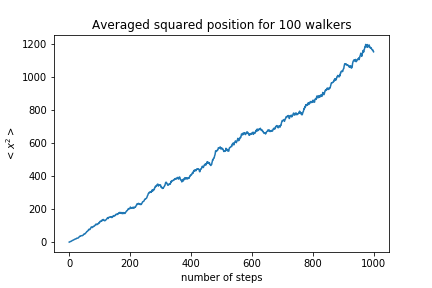
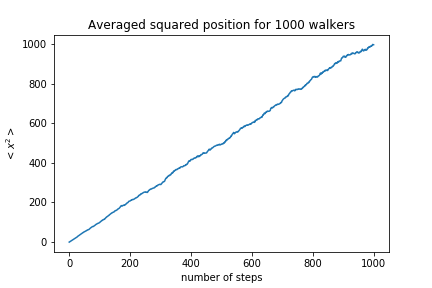
The squared distance is proportional to the number of steps, which means the standard deviation of the walkers position scales like $\sqrt{N}$.
This matches the properties of the solutions of the diffusion equation
$$\frac{\partial \rho}{\partial t} = D \Delta \rho ;,\qquad \Delta \rho = \sum_i \frac{\partial^2\rho}{\partial x_i^2} $$
So random walks are suitable to model diffusion processes.
in multiple dimensions
We can have random walks in more than one dimension
- at each step we decide
- in which dimension to move
- whether to move in the positive or negative direction


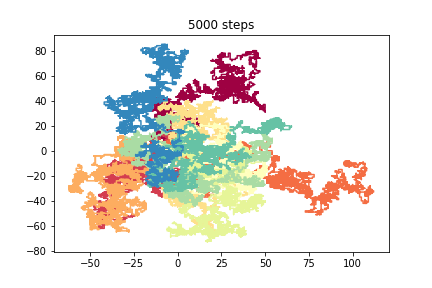
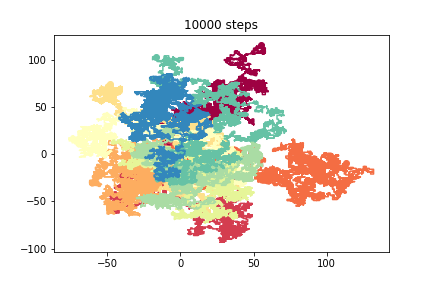
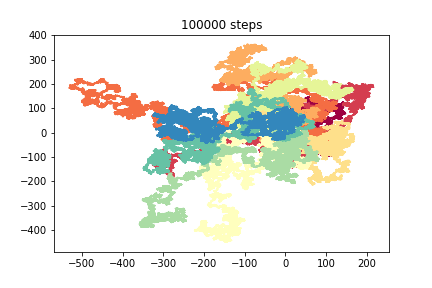
3D walkers
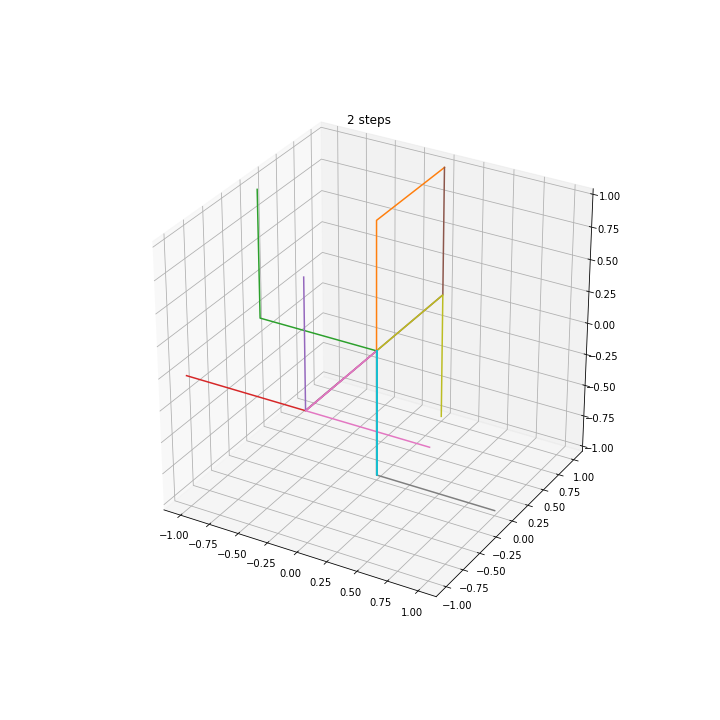
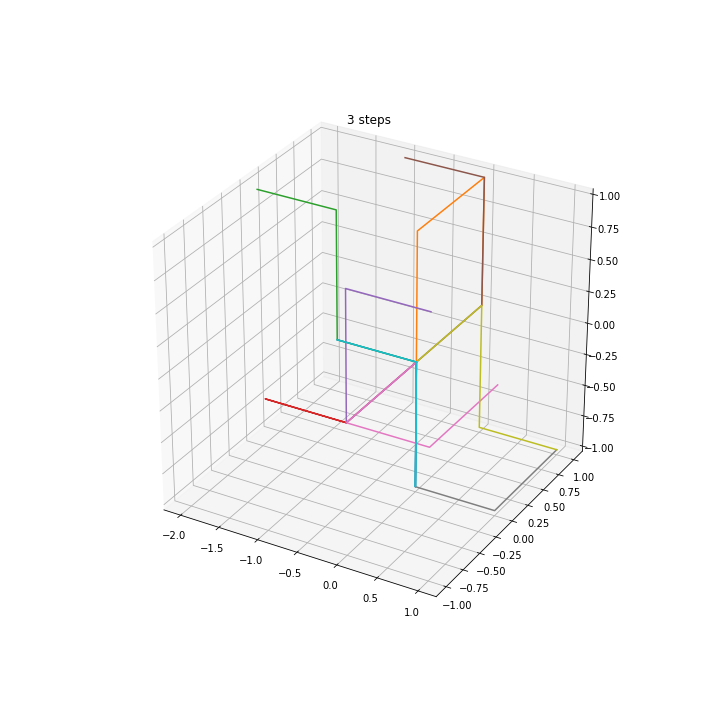
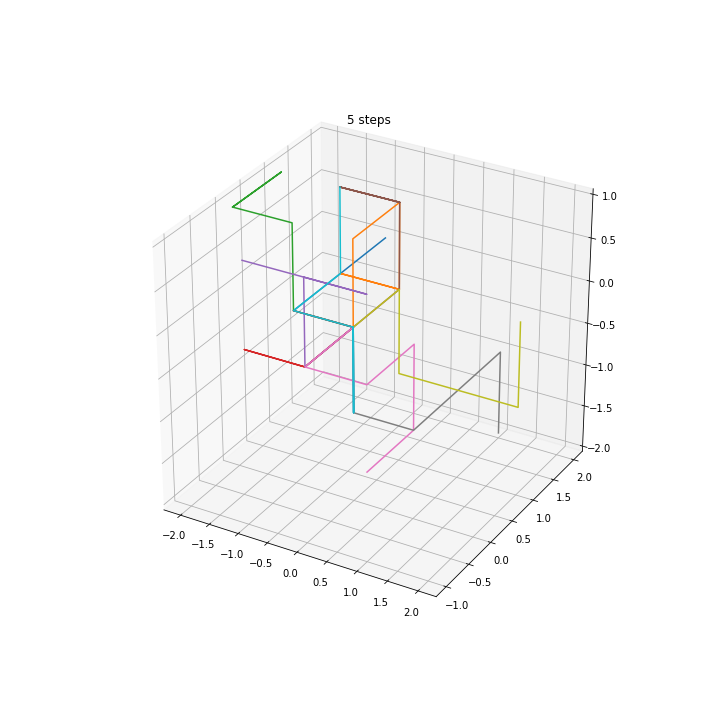
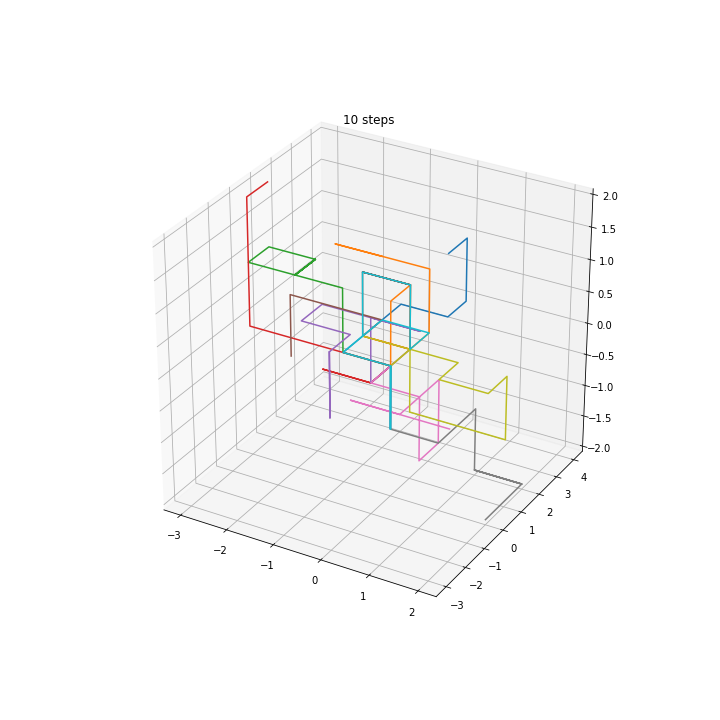
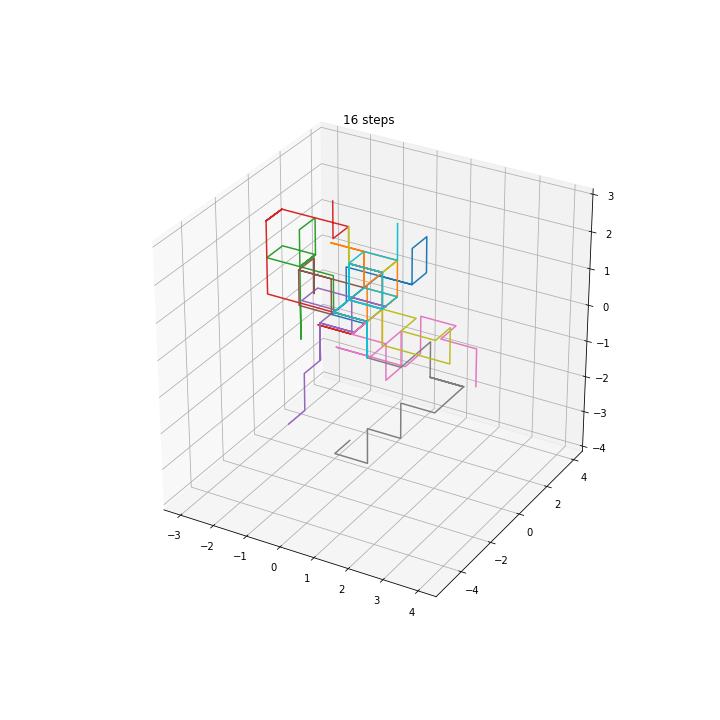
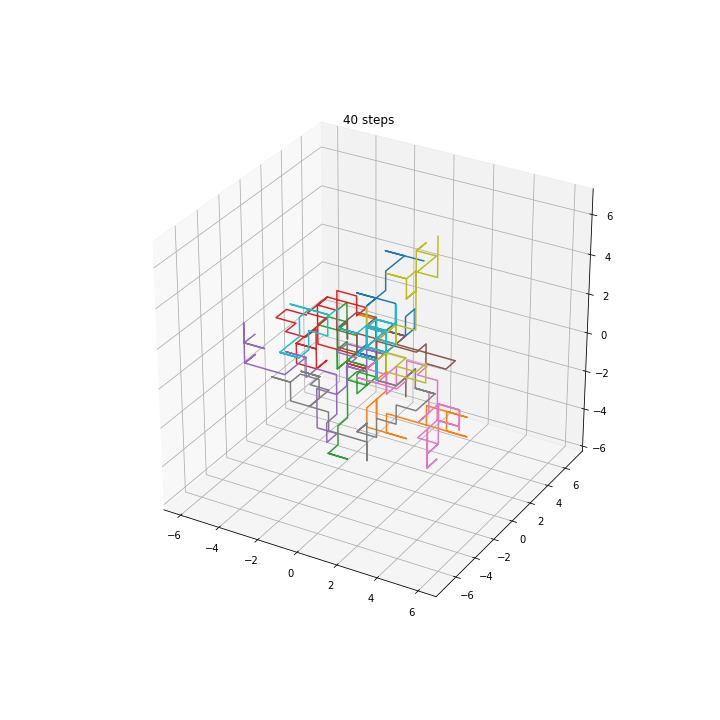
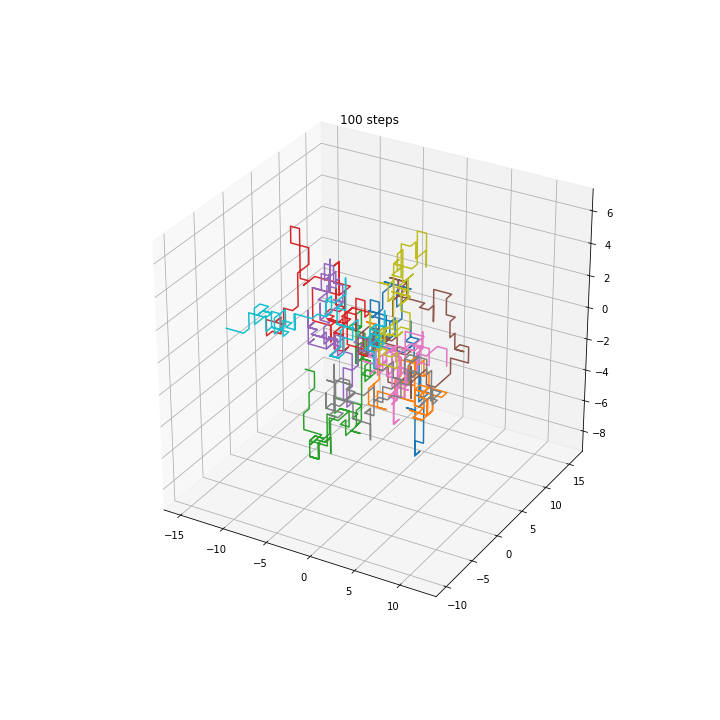
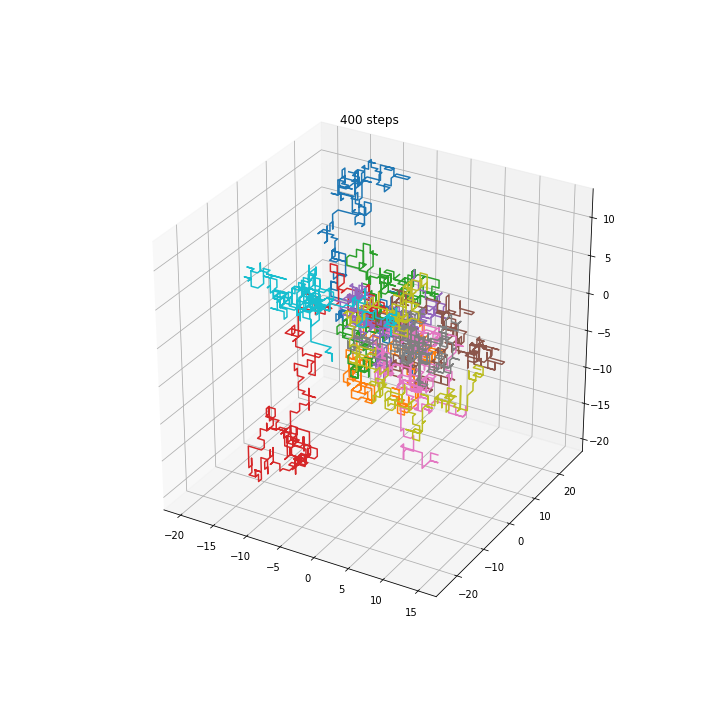
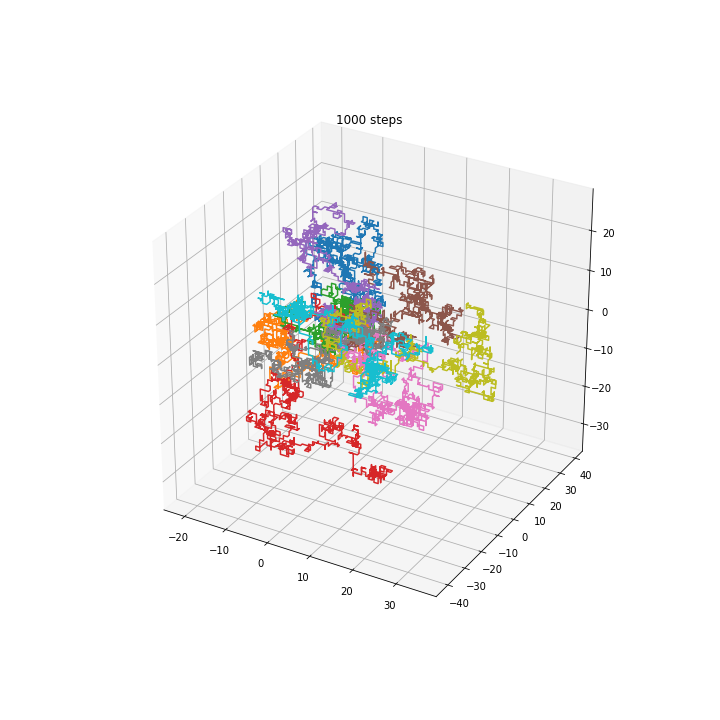
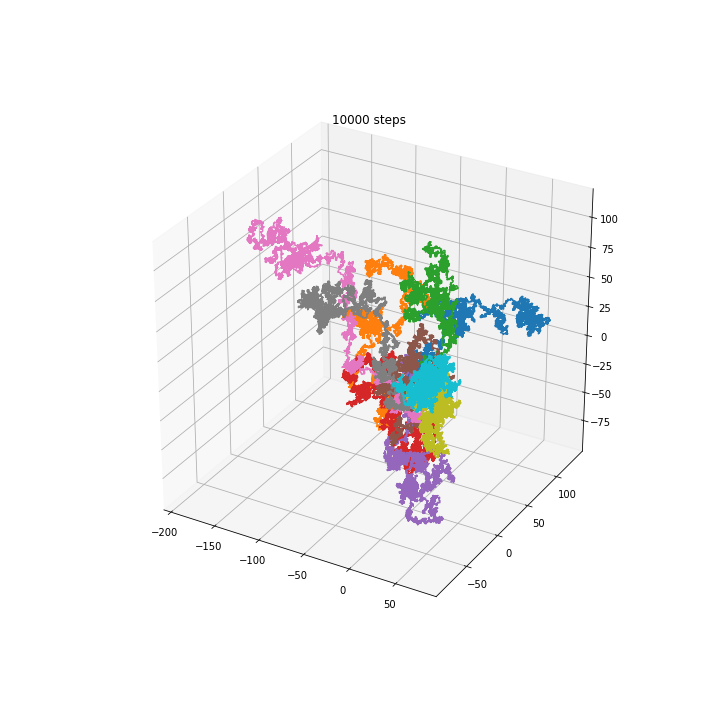
Squared distance in multiple dimensions
The scaling of the squared distance as a function of the number of steps is the same in all dimensions: