Monte Carlo Methods
Motivation
We solved the radioactive decay problem in the continuum limit
In fact the differential equation is for the continuum limit
We can’t formulate a differential equation for a single atom!
Discrete jump from “not decayed yet” to “decayed” is not continous
QM is not predictable we can only say something about the probability of
- some process to happen
- some particle to be measured at some place
- some momentum to be in a certain range
Need to model random processes!
Monte Carlo Methods model processes dictated by “chance”

Monte carlo methods are used when
- deterministic solution is not possible
- deterministic not feasible
Example: Heads or tail
If you have a fair coin you have:
$$P(\rm{heads}) = P(\rm{tails}) = 0.5$$
Continuum behaviour after $N$ tosses:
$$ N_{\rm{tails}}= N ,P(\rm{tails}) $$
To model a coin toss in a computer code we can use the algorithm
- pick a random number $r$ between 0 and 1
- if $r<0.5$ call it “heads”
- else call it tails
import random
r = random.random()
if r < 0.5:
print("Heads")
else:
print("Tails")
Heads
Random numbers on a computer
A computer is supposed to follow completly logical steps in a reliable and reproducible manner
How can we get random numbers out of such a system?
Two ways:
- add some hardware that has some true random source
- radioactive source
- thermal element
- settle for random-looking numbers
Pseudo-random numbers
A pseudo random number generator can create a series of numbers that
- appear random
- but are generated in a reproducible way In most cases they are all we need
Sometimes even better!
Because they are reproducible we can investigate problems more easily.
Qualities we want of a random number generator
- uniform
- no correlations
Anything wrong with this sequence of random numbers?
0.9832267678460693 0.2203662995876763 0.5037457350292935
0.2911137865294745 0.8357817407439925 0.0419691134185419
0.5154070108633051 0.3943863586181417 0.6730444827985615
0.0742773193541438 0.5915453237049658 0.0572064848443438
0.9824507804581079 0.0322811404885930 0.7705440927755651
0.0444644149953312 0.7895013430936832 0.1347927519097241
0.7405181856832592 0.1776195737214916 0.6245760606806046
0.2650806034557952 0.5096497831548584 0.2540509628898961
0.7364134626737031 0.1886737203862982 0.5270875993230715
0.2786651187207341 0.5721228608009541 0.4686535423481123
0.5706138822082498 0.1526963541438493 0.5197948121139808
0.0886715176391272 0.5772852573553948 0.4773593278511974
0.5205314031359037 0.1930917641679141 0.6747961509818463
0.2379674540658641 0.8914451447612017 0.2354200626544225
0.7197981988398199 0.3905317988962405 0.9073705801288487
0.0928109303724942 0.7180298967997073 0.0597337035056059
0.7426005764932174 0.4088670008509029 0.8281958112697092
0.3513294745241624 0.9049702918656014 0.0785847923920087
0.5774232478735082 0.4202395825972462 0.8600639899205031
What would happen if I played head and tails using this sequence?
Anything wrong with this sequence?
0.9340324366518361 0.1942452239758620 0.8298772041601081
0.8822262494087305 0.3389889468301139 0.4509975096682632
0.0070456259245537 0.5874930203333821 0.0560788697075302
0.0009495039349679 0.6221623994563103 0.1197775721080866
0.3884797971270016 0.3792289703359487 0.0220684806817498
0.0335221851689879 0.0130903276329845 0.0002137087429244
0.2369270622811057 0.9310350222585495 0.0041682881249771
0.2927764245430143 0.2170614672860193 0.3617582811578795
0.0079083368035081 0.3352441106121863 0.0726763438695857
0.3096171944471465 0.4155532958746210 0.2313959905774670
0.1261948518760176 0.0620767795787906 0.8714511850852505
0.2055606962048173 0.2810709053139540 0.0003724732597431
0.2581675669811334 3.341114460547e-05 0.0206693607733099
0.2235653013334817 0.1423910910576281 0.0029349521483490
0.3451897478667201 0.0268970573977557 0.3106169935665632
0.0208068282004552 0.8785445710217358 0.5944101164846329
0.9157210006493821 0.0199452814420822 0.0932647062752953
0.0015673383465112 0.0766092137025405 0.6504624209078468
0.0314505521617040 0.0238920440179584 0.9114877115461886
0.0238861352694834 0.6953713549000397 0.0016861540589159
0.1491377175579094 0.1222147775922735 0.1167642156263871
0.6666119229791445 0.2265140367783565 0.6129172054284729
0.2216904236008489 0.6680512255469221 0.7771614309994124
...
Let’s histogram it …
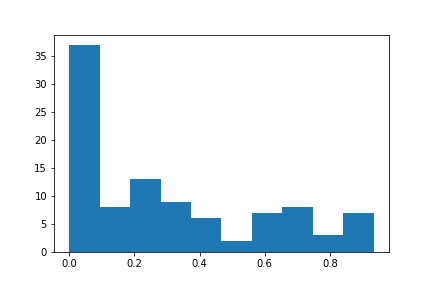
Using the same (bad) PRNG for a while longer we get
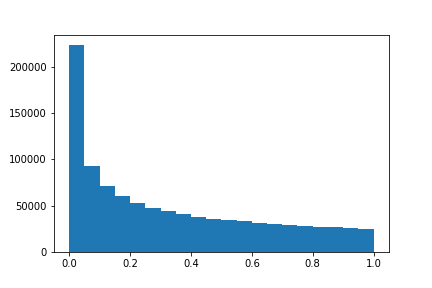
Are the random numbers from python any good?
import matplotlib.pyplot as plt
%matplotlib inline
l = []
for i in range(100000):
l.append(random.random())
plt.hist(l);

State and seeding
A PNRG has a state that is modified after each call, so if you know the state of the generator you can reproduce the series of pseudo random numbers.
The random number generators often use the current time to seed the generator so two sequences are always different.
random.seed(1234)
print(random.random())
print(random.random())
random.seed(1234)
print(random.random())
print(random.random())
0.9664535356921388
0.4407325991753527
0.9664535356921388
0.4407325991753527
Numpy random numbers
Uniform distribution
import numpy
sample = numpy.random.uniform(4, 9, size=(10**6))
plt.hist(sample, bins=numpy.arange(2,10, 0.1));

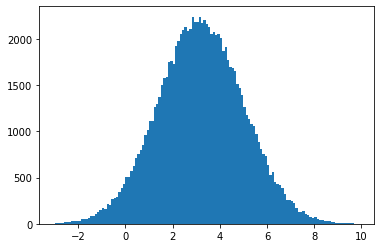
Normal distribution
import numpy
sample = numpy.random.normal(3.2, 1.8, size=(10**5))
plt.hist(sample, bins=numpy.arange(-3, 10, 0.1));
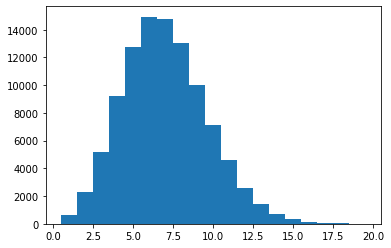
Poisson distribution
import numpy
sample = numpy.random.poisson(7, size=(10**5))
plt.hist(sample, bins=numpy.arange(0.5,20.5, 1.0));
Coin toss
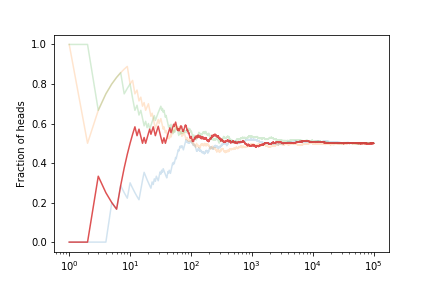
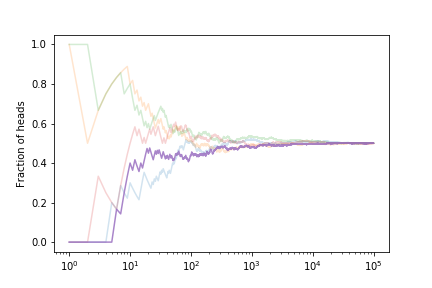
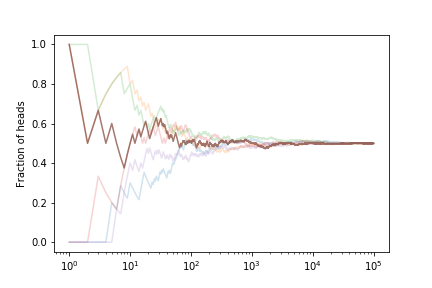
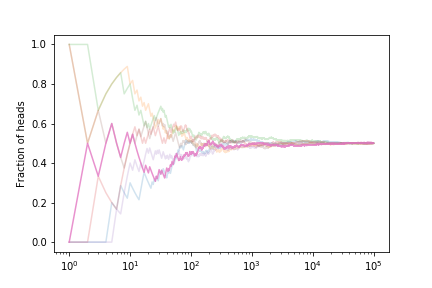
Let’s look at the fraction of heads if we simulate many coin tosses
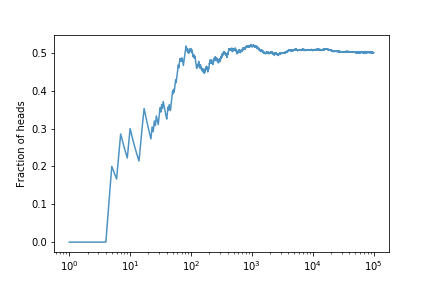
The fraction tends to $ 1/2 $ as expected.
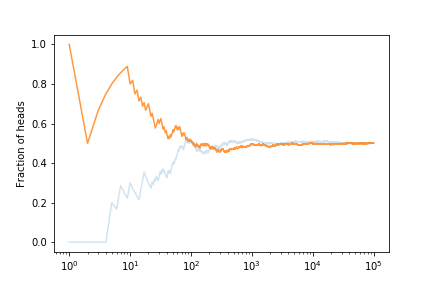
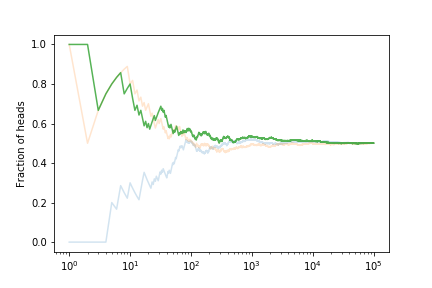
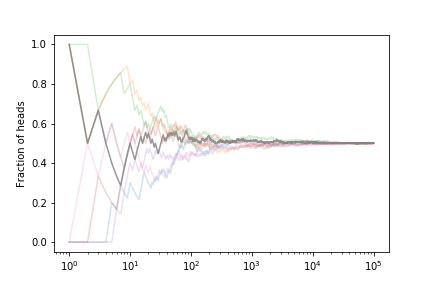
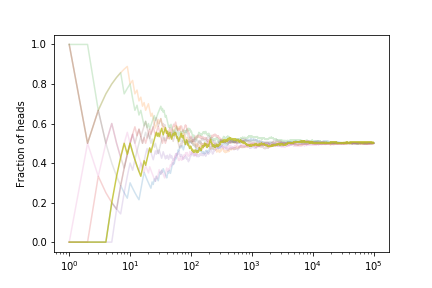
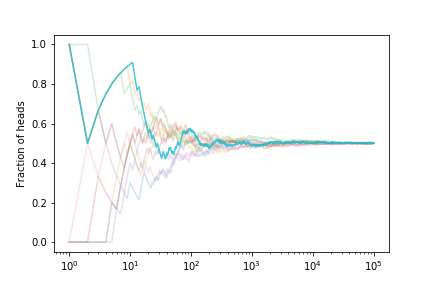
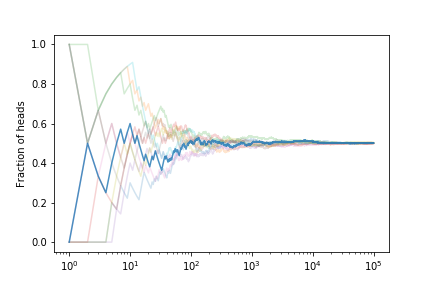
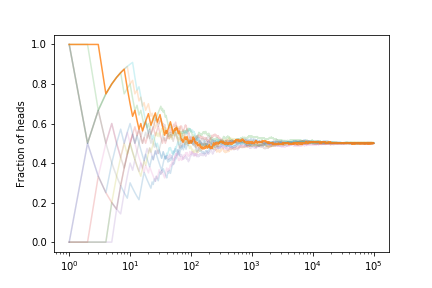
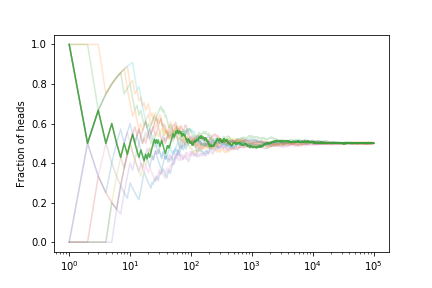
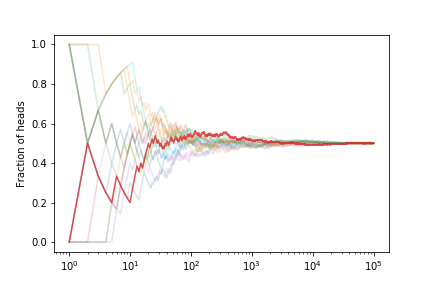
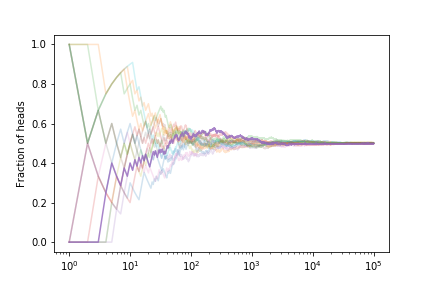
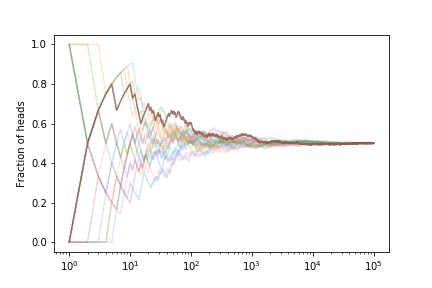
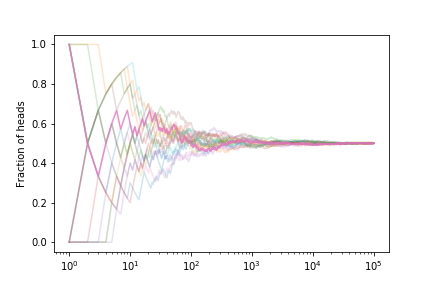
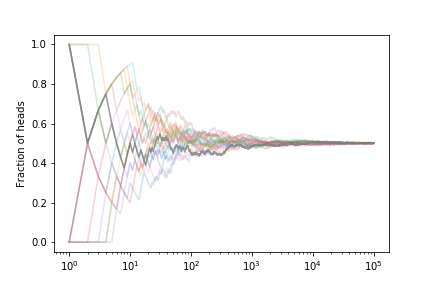
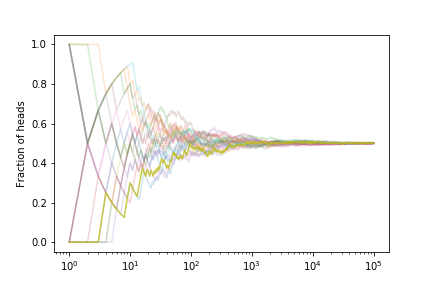
If we estimate the error on the fraction from our set of curves we get
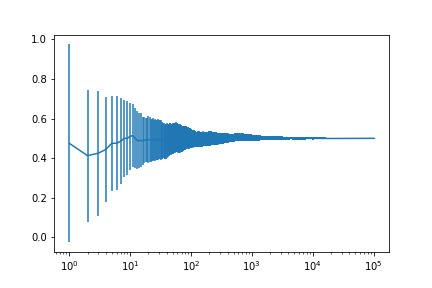
This shows that the expected error on the fraction of heads is decreasing. With what power?
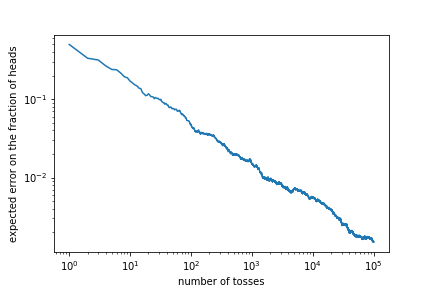
The scaling is $1/\sqrt{N}$
More realistic radioactive decay
Now that we know how to use random numbers to model random process let’s revisit the radioactive decay problem we treated in the continuum limit before.
The probability per time unit of decaying is given by $1/\tau$ where $\tau$ is the mean lifetime.
$$ \frac{dN}{dt}= -\frac{N}{\tau}$$
For a simgle atom, for a small time $\Delta t$ the probability of decaying is given by:
$$p = \frac{1}{\tau} \Delta t $$
For this to be valid we need $\Delta t \ll \tau$. For larger time step we need to integrate:
$$ \frac{1}{\tau}\int_0^{\Delta t} e^{-t/\tau} dt = \left(1-e^{-\Delta t/\tau}\right)$$
We can model the life of a single nucleus by repeating the following steps many times:
- choose a random number $r$
- if $r < p$ the nucleus decays
- otherwise it doesn’t and survives another $\Delta t$
Think of it as a kind of russian roulette…
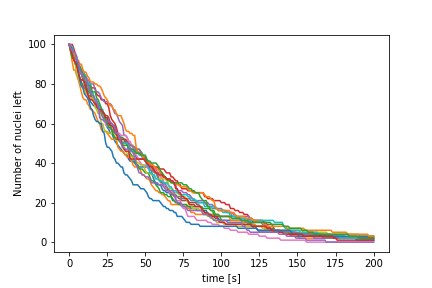
Let’s use a log scale to see that we have something resembling an exponential decay:
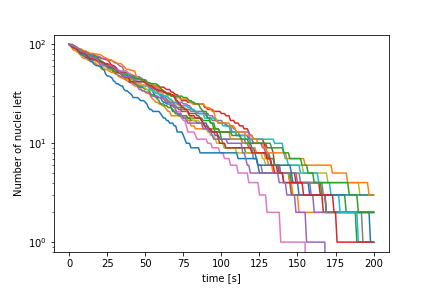
If we increase the number of nuclei we recover the continuum limit:
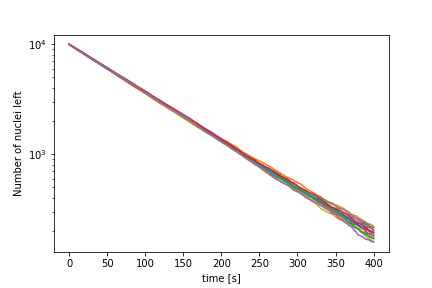
The other extreme is the case of a single nucleus: