Assignment 1
General feedback
Most students did well on this assignment
Remember to use the validate to check your code and you must submit it by clicking submit
Don’t change the import numpy at the top, otherwise the checks will break and you will lose marks.
You only need to import numpy once, not in every cell.
Many students labelled the error axis labeled y-axis, or $sin^2(2x)$, $f(x)$ or even $dx$
Often titles implied that their x-axis is dx, i.e. ‘difference between numerical and analytic vs dx’
Some students made the font size of their x and y labels way bigger to the point they’re off the plot.
Many students picked dx so small that the numerical derivative always evaluated to zero.
The main mistakes were misunderstanding the round off error with the smallest dx.
Model solution
Automatically marked cells:
def f(x):
'''Function equivalent to sin^2(2x), should work for one argument or a numpy array'''
return numpy.sin(2.*x)**2
def df_analytic(x):
'''
The analytic derivative
'''
return 2.*numpy.sin(4.*x)
def central_difference(f, x, dx):
'''
This function implements the central difference method for the
first derivative of the function f at position x using interval
dx.
'''
return 0.5*(f(x+dx)-f(x-dx))/dx
Plotting task
xs = numpy.linspace(-2*numpy.pi,2*numpy.pi,100)
df_dx_1 = central_difference(f, xs, dx=1e-4)
df_dx_2 = central_difference(f, xs, dx=5e-6)
df_dx_3 = central_difference(f, xs, dx=1e-8)
df_dx_analytical = df_analytic(xs)
plt.figure(figsize=(8, 4))
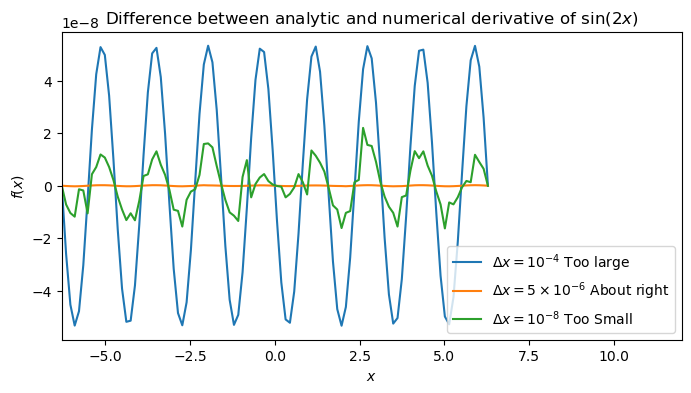
plt.plot(xs, df_dx_1 - df_dx_analytical,label="$\Delta x=10^{-4}$ Too large")
plt.plot(xs, df_dx_2 - df_dx_analytical,label="$\Delta x=5\\times10^{-6}$ About right")
plt.plot(xs, df_dx_3 - df_dx_analytical,label="$\Delta x=10^{-8}$ Too Small")
plt.legend(loc='lower right')
plt.title("Difference between analytic and numerical derivative of $\sin(2x)$")
plt.xlim([-2.*numpy.pi,12])
plt.ylabel("$f(x)$")
plt.xlabel("$x$")
Free text question
For too large a value of $\Delta x$ then our numerical approximation to the derivative is poor and in the plot we see the first neglected term in the Taylor series which is $\propto \frac{d^3f}{dx^3} (\Delta x)^2 \propto \sin(4x) (\Delta x)^2$ which is why we see the sinuosoidal behaviour.
For too small a value of $\Delta x$ then the difference between $f(x+\Delta x)$ and $f(x-\Delta x)$ becomes small and we lose numerical precision on the calculation of the numerator in the central difference giving the jagged result.