Assignment 7

General feedback

Most were good, however a number of students didn’t run enough steps to see the behaviour for the different step sizes in the minimisation. A lot of people lost marks for forgetting to include a title, labels and/or a legend on their plot . Some people also lost marks for providing no explanation for the question answer. Some students used a separate loop to extract the coordinates from the history 2-dimensional array to do the plot. They can more easily extracted using slicing:

trajectory_xs = history[:, 0]
trajectory_ys = history[:, 1]

For the generating part of the Root notebook it was most convenient to use the Newton-Raphson` method as it is very robust. Using other methods tend to take the search for the zero out of the 0-10 interval and cause errors with the square root. Alternatively one can provide a good guess of the zero location for the other methods to avoid the problem.

I have seen this type of code quite often:

x = secant(sigma, 0, 10, 1e-20)[len(secant(sigma, 0, 10, 1e-10))-1]

This is quite wasteful, as one needs to do the same calculation of the zero twice, the second time only to find the length of the array we obtained the first time. Better would be

res = secant(sigma, 0, 10, 1e-20)
x = res[len(res)-1]

where we only calculate the zero once. If one does not need the array of attempts one can do even better with

x = secant(sigma, 0, 10, 1e-20)[-1]

infinite loops

Some students had infinite loops in their code. The marking system cannot cope with that so I had to manually change the code. It is a good idea to introduce a maximum iteration number, especially while debugging potentially infinite loops! See the FAQ about infinite loops.

Autograded cells

Root Finding

def NewtonRaphson(f, df, x0, tolerance):
    '''
       finds a root of the equation f(x)=0, df is the derivative of f.
       The function should stops iterating when 
       
            | x_{i+1} - x_{i} | < tolerance
            
        and return an array with all the x_i values.
        
        x_0 is the starting point.
                
    '''
    xs = [ x0 ]
    x=x0
    while True:
        x = x - f(x)/df(x)
        xs.append(x)
        if abs( xs[-1] - xs[-2]) < tolerance:
            return xs

def bisect(f,x0,x1,tolerance):
    '''
    finds a root of the equation f(x)=0, x0 and x1 are
    the first two values, they have to have different signs!
    It should not matter which one corresponds to a positive 
    value of f. 
    
    The iteration terminates when the length of the interval
    between the upper and lower limit is smaller than the tolerance
    
    The list returned should contain all points the algorithm calculates using the middle of the interval.  
    '''

    f0=f(x0)
    f1=f(x1)

    if f0>0:
        xpos=x0
        xneg=x1
    else:
        xpos=x1
        xneg=x0        
    
    xs=[]
    vs=[]
    
    while True:
        if abs(xpos-xneg)<tolerance:
            return xs
        xnew=(xpos+xneg)/2
        xs.append(xnew)
        fnew=f(xnew)
        if fnew>0:
            xpos=xnew
        else:
            xneg=xnew

def generate(xis):
    sample = []
    for xi in xis:
        def toSolve(x):
            return cumulative(x)- xi
        zero = NewtonRaphson(toSolve,pdf,0.0,1e-9)[-1]
        sample.append(zero)
    return sample

Gradient descent

def f(r):
    '''Function to be minimised'''
    x, y = r
    return (1 - x)**2 + 100*(y - x**2)**2
    
    
def grad(r):
    '''Calculate gradient of banana function at coordinates r = (x,y)'''
    x, y = r
    partial_x = -2*(1-x) - 400*x*(y-x**2)
    partial_y = 200*(y-x**2)
    
    return numpy.array([partial_x, partial_y])

def gradientDescent(df, r0, eta, nstep):
    xy = r0
    history = numpy.empty( (nstep+1, 2) )
    history[0] = xy 
    for i in range(nstep):
        der = df(xy)
        xy = xy - eta * der
        history[i+1] = xy
    return history

Plot examples

here are example plots for the assignment:

Gradient descent

# Generate banana function
N = 100 # Resolution of 2D image
x0 = -0.2
x1 = 1.2
y0 = 0
y1 = 1.2
xs = numpy.linspace(x0, x1, N)
ys = numpy.linspace(y0, y1, N)
dat = numpy.zeros((N, N))

for ix, x in enumerate(xs):
    for iy, y in enumerate(ys):
        r = [x,y]
        dat[iy, ix] = f(r)

plt.figure(figsize=(8,8))
im = plt.imshow(dat, extent=(x0, x1, y0, y1), origin='lower', cmap=matplotlib.cm.gray, 
                norm=matplotlib.colors.LogNorm(vmin=0.01, vmax=200))
plt.colorbar(im, orientation='vertical', fraction=0.03925, pad=0.04)

# Now generate the trajectories:
gammas = [0.004, 0.003, 0.002]  # Gammas to try out
r0 = numpy.array([0.2, 1])  # Initial seed point


### BEGIN SOLUTION ###
for gamma in gammas:
    trajectory2 = gradientDescent(grad, r0, gamma,2000)
    trajectory2_xs = trajectory2[:, 0]
    trajectory2_ys = trajectory2[:, 1]

    plt.plot(trajectory2_xs, trajectory2_ys, '-o', lw = 1,  label='$\gamma =$%.3f' % (gamma,))

plt.xlabel('$x$')
plt.ylabel('$y$')
plt.legend();
### END SOLUTION ###

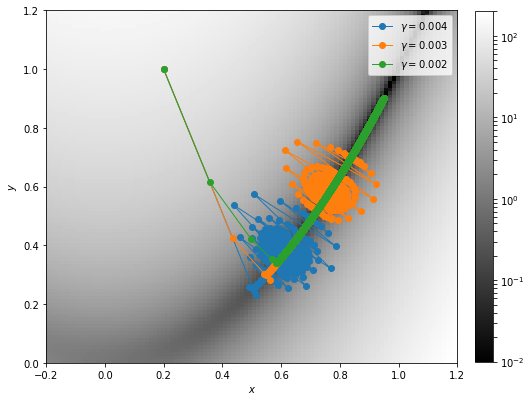
The value of $\eta$ that works best is $0.002$. For the other values the gradient descent starts to oscillate before reaching the minimum. $\eta$ can be seen as the resolution with which the algorithm “feels” the slope and for too large values the algorithm does not see that there is a small slope in the bottom of the valley.