Assignment 4
General Feedback
Some students did not set a limit on y in the trajectory plot leading to negative values of y, which are unphysical as the cannon ball has hit the ground.
Some students did not use a large enough value for the final time, resulting in most of the projectiles not reaching the ground.
Some students solved the “no air resistance” problem analytically. It is more practical to use the existing code in the relevant limit (kappa = 0 or rho_air = 0).
Some students did not read the plotting instructions carefully and plotted the trajectories for a second time but this time without drag.
Some students plotted the range on the x-axis and velocity on the y-axis. Normally the independent variable, i.e. the one you are changing should be on the x-axis and the dependent variable, the one you measure, on the y-axis.
Some students were still missing labels, title or a legend
Model solution
Automatically marked tasks
def get_area(r):
'''
This function returns the cross section area of a sphere of radius r. The returned
value is in the squared units of the unit of the radius argument.
'''
### BEGIN SOLUTION ###
area = numpy.pi * r**2 # Cross sectional area of sphere
return area
### END SOLUTION ###
def get_mass(r):
'''
This function returns the mass of an iron sphere of radius r. The radius
should be given in meter and the return value is in kg.
'''
### BEGIN SOLUTION ###
mass = rho_iron * (4/3) * numpy.pi * r**3 # Mass of sphere
return mass
### END SOLUTION ###
area_cb = get_area(r_cb)
mass_cb = get_mass(r_cb)
def f(r, t):
'''Implements differential equation for cannonball from state vector r and time t'''
# Unpack array of the state
x, y, qvx, vy = r
# these variables should updated in your code to be the derivatives of
# the x, y positions and the derivative of the x, y velocities.
dx_t, dy_dt, dvx_dt, dvy_dt = 0, 0, 0, 0
### BEGIN SOLUTION ###
v = numpy.sqrt(vx**2 + vy**2)
k = 0.5 * rho_air * kappa * area_cb
# x-components
dx_dt = vx # DE for x position
dvx_dt = -(k/mass_cb)*v*vx # DE for x velocity
# y-components
dy_dt = vy # DE for y position
dvy_dt = -(k/mass_cb)*v*vy - g
### END SOLUTION ###
return numpy.array([dx_dt, dy_dt, dvx_dt, dvy_dt])
def solve_euler(state_initial, t1, n_steps):
'''Solves ODE using Euler's method from state_initial to end time t1 using n_panels panels'''
# Define array for trajectory history
history = numpy.empty((n_steps+1,4)) # Number of columns is equal to number of variables to solve for (4)
history[0] = state_initial
# you should now populate the history array
### BEGIN SOLUTION ###
# Define necessary local variables
t = 0
dt = t1 / n_steps # Panel size
for i in range(n_steps):
t = i*dt
history[i+1] = history[i] + f(history[i], t) * dt
### END SOLUTION ###
return history
def find_zero_linear(x1, x2, y1, y2):
if y1*y2 > 0:
print("I expect y1 and y2 to have opposite signs!")
### BEGIN SOLUTION ###
return (x1*y2 - x2*y1 )/(y2 - y1)
### END SOLUTION ###
Plotting tasks
These are examples for the plotting tasks.
n_steps = 1000
max_time = 300
v0s = numpy.linspace(50, 1000, 20)
ranges = []
ranges_noresistance = []
theta = numpy.deg2rad(60)
v0 = 125
n_steps = 1000
thetas = range(5, 90, 5)
t1=100
# Loop creating trajectories
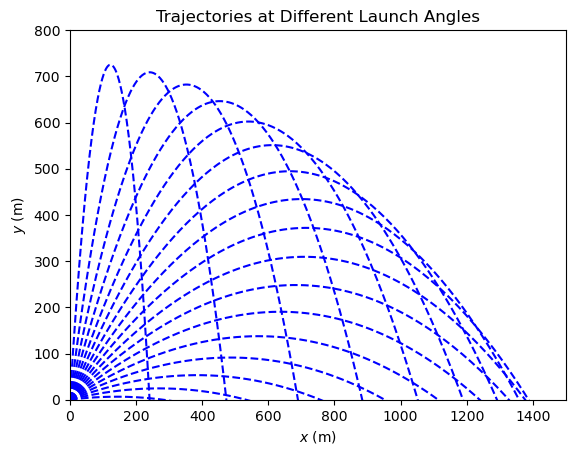
for theta in thetas:
theta = numpy.deg2rad(theta) # numpy trig functions work in radians
vx, vy = v0*numpy.cos(theta), v0*numpy.sin(theta)
initial_conditions = [0, 0, vx, vy]
values_euler = solve_euler(initial_conditions, t1, n_steps)
# Plot trajectories
xs_euler, ys_euler = values_euler[:,0], values_euler[:,1]
plt.plot(xs_euler, ys_euler, color='blue', linestyle='--')
plt.xlim(0,1500)
plt.ylim(0,800)
plt.title('Trajectories at Different Launch Angles')
plt.xlabel('$x$ (m)')
plt.ylabel('$y$ (m)')
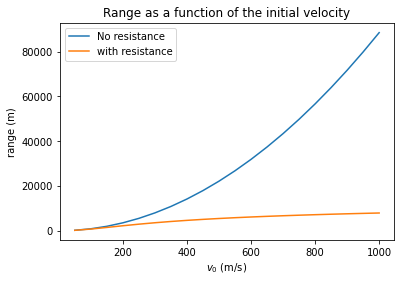
n_steps = 1000
max_time = 300
v0s = numpy.linspace(50, 1000, 20)
ranges = []
ranges_noresistance = []
theta = numpy.deg2rad(60)
for v0 in v0s:
vx, vy = v0*numpy.cos(theta), v0*numpy.sin(theta)
initial_conditions = [0, 0, vx, vy]
rho_air = 0
history = solve_euler(initial_conditions, max_time, n_steps)
rng = find_range(history)
ranges_noresistance.append(rng)
rho_air = 1.23
history = solve_euler(initial_conditions, max_time, n_steps)
rng = find_range(history)
ranges.append(rng)
plt.plot(v0s,ranges_noresistance,label="No resistance")
plt.plot(v0s,ranges, label="with resistance")
plt.title('Range as a function of the initial velocity')
plt.xlabel('$v_0$ (m/s)')
plt.ylabel('range (m)')
plt.legend()
Using scipy
As with last week’s assignment we can use scipy to solve the problem, it’s a bit more tricky as we need the solution at intermediate time steps.
import scipy.integrate as integrate
def f_swap(t,n) :
return f(n,t)
n_steps = 1000
max_time = 300
v0s = numpy.linspace(50, 1000, 20)
ranges = []
ranges_noresistance = []
theta = numpy.deg2rad(60)
times=numpy.linspace(0,max_time,n_steps+1)
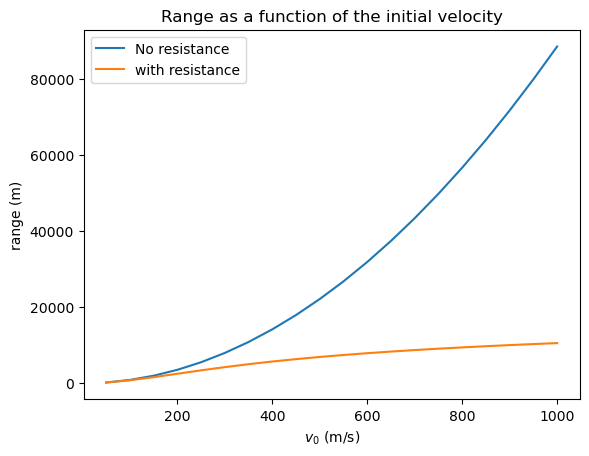
for v0 in v0s:
vx, vy = v0*numpy.cos(theta), v0*numpy.sin(theta)
initial_conditions = numpy.array([0, 0, vx, vy])
rho_air = 0
output = integrate.solve_ivp(f_swap,(0,max_time),initial_conditions,t_eval=times,rtol=1e-9)
history = numpy.transpose(output.y)
rng = find_range(history)
ranges_noresistance.append(rng)
rho_air = 1.23
output = integrate.solve_ivp(f_swap,(0,max_time),initial_conditions,t_eval=times,rtol=1e-9)
history = numpy.transpose(output.y)
rng = find_range(history)
ranges.append(rng)
plt.plot(v0s,ranges_noresistance,label="No resistance")
plt.plot(v0s,ranges, label="with resistance")
plt.title('Range as a function of the initial velocity')
plt.xlabel('$v_0$ (m/s)')
plt.ylabel('range (m)')
plt.legend();