Assignment 3

General Feedback

The assignment was solved well in general but here are some common problems that occurred.

  • many people used a linear scale to generate the data for the error plot. If you are going to plot on a log scale it is more efficient to use points equidistant on a log scale. Some people did not make a log-log plot.

  • some did not realise that one needs to use a fixed time interval to evolve the ODE over (for example from t=0 to t=1000) and therefore one has to change the size of dt like dt = (t1 - t0) / n_steps to adapt to changing the number of steps. The time used for the analytical reference value should also match!

  • one elegant way of accessing the last element in an array or list a is to use -1 as the index.

  • some students, instead of using the final value in the numerical array (i.e. Value at time t_final) to calculate the error, took either some sort of an average of the errors or took the maximum error (doing numeric_vals - analytic and taking the maximum)

  • a significant number of students had a very small t_final (e.g. 1, 5 or 10), which made the RK4 curve almost flat and the scaling was not clear.

a = [ 1, 2, 3, 4, 5, 6, 7, 8]
last_element = a[-1]

  • always use the functions you had written, and importantly tested, at the start. Don’t copy the code further down the notebook. At best this is inefficient, at worst if can lead to mistakes.

  • Some students were still missing labels, title or a legend, or labelling axes as log when a log scale had been used (you should only put log in the label if you have taken and plotted the logs)

  • Some students had issues in the code, such as undefined variables. Make sure you run validate or ‘restart and run all’ to check for this.

Model solution

Automatically marked cells:

# define a function to calculate the mean lifetime from the half life
def meanLifetime(halfLife):
    mean = halfLife/ np.log(2)
    return mean

T_HALF = 5730.
TAU = meanLifetime(T_HALF)


def f_rad(N, t):
    return - N / TAU

def analytic(N0, t):
     return N0 * numpy.exp(-t/TAU)

def solve_euler(f, n0, t0, dt, n_panels):
    # Initialise variables
    n = n0
    t = t0
    n_t = numpy.empty((n_panels+1))  # Array ready for updated counts
    
    # For loop generating decay data in n_panels steps of width dt using Euler's method
    for i in range(n_panels+1):
        n_t[i] = n
        n += dt*f(n, t)
        t += i*dt  # For completeness, but this ODE does not need time.
    return n_t

def solve_RK4(f, n0, t0, dt, nsteps):
    res_n = numpy.array([0.0] * ( nsteps + 1 ))

    current_n = n0
    current_t = t0
    
    res_n[0] = current_n
    
    for i in range(1,nsteps+1):
        
        k1 = f(current_n          , current_t)
        n1 = current_n + k1* dt/2.0
        k2 = f(n1, current_t + dt/2.0)
        n2 = current_n + k2* dt/2.0
        k3 = f(n2, current_t + dt/2.0)
        n3 = current_n + k3* dt
        k4 = f(n3, current_t + dt )
        k = 1.0/6.0 * ( k1 + 2 * k2 + 2 * k3 + k4 )
        current_n += dt * k
        current_t += dt
        res_n[i] = current_n
    return res_n

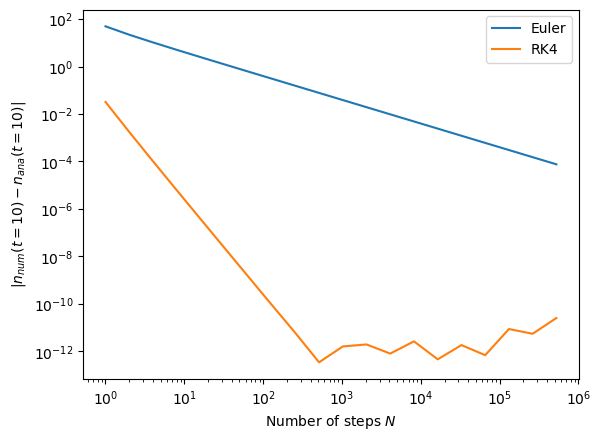
Plotting task

This is an example for the plotting task.

n0 = 1000
tmax = 3000.
target = analytic(n0, tmax )
err_euler = []
err_rk4 = []
ntest = [ 2**expo for expo in range(20) ] 
for n_step in ntest:    
    res_euler = solve_euler(f_rad,n0, 0, tmax/n_step, n_step)
    res_rk4 = solve_RK4(f_rad,n0, 0, tmax/n_step, n_step)
    err_euler.append( abs( res_euler[-1] - target) )
    err_rk4.append( abs( res_rk4[-1] - target) )
    
plt.plot(ntest, err_euler, label='Euler')    
plt.plot(ntest, err_rk4, label='RK4')    
plt.loglog()
plt.legend()
plt.xlabel('Number of steps $N$')
plt.ylabel('$|n_{num}(t=3000)-n_{ana}(t=3000)|$');

png

Using scipy

Again if we really had to solve this problem we would use scipy. The solve_ivp function provides access to a range of different methods. The default is called RK54 which uses the 5th order Runge-Kutta method to compute the values together with the 4th order to estimate the error. It needs the function for the derivative to have both the value and the time, this is why ours had this, although in the opposite order.

import scipy.integrate as integrate
def f(t,n) :
    return f_rad(n,t)
output = integrate.solve_ivp(f,(0,tmax),np.array([n0]),rtol=1e-9)
print((output.y[0][-1]-target)/target)

    1.3500933701583496e-10